CALCULATE
Ouvrier
Bonjour à tous,
Il s'agit d'un arc et la théorie de Lobatchevsky permet de calculer le plan tangent et la courbure en chaque point de l'arc. La seule condition est de connaître l'équation de cet arc, sans équation aucune possibilité. Il faut oublier la géométrie classique d'Euclide qui ne donnera rien (en plus le cinquième axiome d'Eucide est inexact). Il y a plus de 40 ans j'avais étudié les arcs dans une forme quelconque, et pour application je m'étais servi de l'arc circulaire, mais on peut prendre l'arc que l'on veut. Je donne ici les débuts de calculs, pas pour montrer ce que je sais non car en 40 ans j'ai grandi et certaines choses sont inexactes selon moi, mais pour montrer que l'on est capable de le faire.....mais hélas avec une équation !!!!! Une fois l'équation connue on pourra calculer exactement en un certains nombres de points la tangence et la courbure grace à cette théorie. Je reconnais que pour quelqu'un qui n'est pas habitué cela semble très complexe, mais bon c'est ainsi je n'y peux rien.....sinon utiliser la théorie approchée de Dodore.
A +
Calculate


Il s'agit d'un arc et la théorie de Lobatchevsky permet de calculer le plan tangent et la courbure en chaque point de l'arc. La seule condition est de connaître l'équation de cet arc, sans équation aucune possibilité. Il faut oublier la géométrie classique d'Euclide qui ne donnera rien (en plus le cinquième axiome d'Eucide est inexact). Il y a plus de 40 ans j'avais étudié les arcs dans une forme quelconque, et pour application je m'étais servi de l'arc circulaire, mais on peut prendre l'arc que l'on veut. Je donne ici les débuts de calculs, pas pour montrer ce que je sais non car en 40 ans j'ai grandi et certaines choses sont inexactes selon moi, mais pour montrer que l'on est capable de le faire.....mais hélas avec une équation !!!!! Une fois l'équation connue on pourra calculer exactement en un certains nombres de points la tangence et la courbure grace à cette théorie. Je reconnais que pour quelqu'un qui n'est pas habitué cela semble très complexe, mais bon c'est ainsi je n'y peux rien.....sinon utiliser la théorie approchée de Dodore.
A +
Calculate


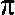 que le Covid 19, qui était une partie de plaisir à côté.
que le Covid 19, qui était une partie de plaisir à côté.