SULREN
Compagnon
Bonsoir,
Reste à définir le domaine à couvrir et à …..trouver le temps pour faire le travail (c'est la seule vraie diffficulté, à mon avis).
La totalité du domaine qu’il faudrait couvrir pour être exhaustif peut être défini comme suit :
Tu sais mieux que nous les nombres de rangées de trous sur les disques des constructeurs de machines outil, puisque tu as fait une synthèse de tout ce que tu as trouvé.
Cela démarre à14 trous et monte à 49 trous pour plusieurs d’entre eux, à 89 pour d’autres et à 199 trous pour CINCINATTI.
On peut décider de couvrir la totalité des possibilités, donc :
- De pouvoir faire la division en utilisant deux cercles de trous quelconque, pris dans toute cette gamme de 14 à 199 trous. Cela signifie qu’on couvre aussi le cas du diviseur à deux plateaux.
- De prendre en compte les mouvements additifs et aussi les soustractifs.
- De prévoir les trois cas de rapport de réduction les plus courants : 1 :40 , 1 :60 , 1 :90
- De trouver les solutions pour les divisions allant de 2 à 400
Cela est moulinable. Quand je fais ce genre d’exercice je préfère utiliser un PC tour, super bien ventilé, plutôt qu’un portable, parce que l’unité centrale tourne plein pot et chauffe un max.
(Je l'ai fait pour des calculs de trains d'engrenages permettant d'obtenir des rapports de réduction extrêmement prècis : genre nombre pi avec 14 décimales et avec des précisions du 1/100 de milliardième. C'était pour des rouages d'horloges astronomiques).
Je l'ai fait aussi pour la résolution numérique de systèmes d'équations non linéaires).
Le gros problème (déjà signalé) c’est la masse des solutions qui en résulteront. Même avec de bons critères de sélection on devra peut-être sélectionner pour chacun des 3 rapports, 100 à 200 solutions (à voir) pour chacune des 400 divisions à traiter, afin de permettre aux utilisateurs d’en trouver au moins une qui corresponde aux disques dont ils disposent.
Impossible de mettre cela sur des tableaux papiers, seulement dans des fichiers.
@simon74 saura le dire mieux que moi, mais il me semble qu’il faudra un fichier de plusieurs Mega Oct pour chacun des 3 rapports.
Sous forme papier cela ferait un bouquin, sur une clé USB c’est nada.
Deuxième problème, il faut retrouver les solutions correspondant aux données de l’utilisateur.
Il faut donc mettre à sa disposition un petit executable tournant sur l’OS de son PC, avec une petite interface de saisie :
R : rapport du diviseur
Z : nombre de dents à tailler
Liste des disques à trous disponibles dans ses tiroirs.
La liste des solutions correspondant à ses critères sera alors automatiquement extraite et lui sera présentée sur l'écran.
Il faudra aussi inclure un petit fichier ReadMe qui l’informera sur les notions de précisions et autres choses fondamentales à savoir.
Mais je ne suis pas informaticien, juste un …..« neo-rural »…. un peu « bricoleur du dimanche ».
D’autres membres, dont @simon74, définiront ces volumes mieux que moi.
Je pense que je sais faire et que @simon74 sait faire aussi. Il vient de le prouver.Je ne suis pas d'accord !
Au point où vous en êtes, il faut donner les meilleures solutions possibles, sans se préoccuper si j'ai ou pas, si je peux monter deux plateaux ou pas.
Reste à définir le domaine à couvrir et à …..trouver le temps pour faire le travail (c'est la seule vraie diffficulté, à mon avis).
La totalité du domaine qu’il faudrait couvrir pour être exhaustif peut être défini comme suit :
Tu sais mieux que nous les nombres de rangées de trous sur les disques des constructeurs de machines outil, puisque tu as fait une synthèse de tout ce que tu as trouvé.
Cela démarre à14 trous et monte à 49 trous pour plusieurs d’entre eux, à 89 pour d’autres et à 199 trous pour CINCINATTI.
On peut décider de couvrir la totalité des possibilités, donc :
- De pouvoir faire la division en utilisant deux cercles de trous quelconque, pris dans toute cette gamme de 14 à 199 trous. Cela signifie qu’on couvre aussi le cas du diviseur à deux plateaux.
- De prendre en compte les mouvements additifs et aussi les soustractifs.
- De prévoir les trois cas de rapport de réduction les plus courants : 1 :40 , 1 :60 , 1 :90
- De trouver les solutions pour les divisions allant de 2 à 400
Cela est moulinable. Quand je fais ce genre d’exercice je préfère utiliser un PC tour, super bien ventilé, plutôt qu’un portable, parce que l’unité centrale tourne plein pot et chauffe un max.
(Je l'ai fait pour des calculs de trains d'engrenages permettant d'obtenir des rapports de réduction extrêmement prècis : genre nombre pi avec 14 décimales et avec des précisions du 1/100 de milliardième. C'était pour des rouages d'horloges astronomiques).
Je l'ai fait aussi pour la résolution numérique de systèmes d'équations non linéaires).
Le gros problème (déjà signalé) c’est la masse des solutions qui en résulteront. Même avec de bons critères de sélection on devra peut-être sélectionner pour chacun des 3 rapports, 100 à 200 solutions (à voir) pour chacune des 400 divisions à traiter, afin de permettre aux utilisateurs d’en trouver au moins une qui corresponde aux disques dont ils disposent.
Impossible de mettre cela sur des tableaux papiers, seulement dans des fichiers.
@simon74 saura le dire mieux que moi, mais il me semble qu’il faudra un fichier de plusieurs Mega Oct pour chacun des 3 rapports.
Sous forme papier cela ferait un bouquin, sur une clé USB c’est nada.
Deuxième problème, il faut retrouver les solutions correspondant aux données de l’utilisateur.
Il faut donc mettre à sa disposition un petit executable tournant sur l’OS de son PC, avec une petite interface de saisie :
R : rapport du diviseur
Z : nombre de dents à tailler
Liste des disques à trous disponibles dans ses tiroirs.
La liste des solutions correspondant à ses critères sera alors automatiquement extraite et lui sera présentée sur l'écran.
Il faudra aussi inclure un petit fichier ReadMe qui l’informera sur les notions de précisions et autres choses fondamentales à savoir.
Mais je ne suis pas informaticien, juste un …..« neo-rural »…. un peu « bricoleur du dimanche ».
D’autres membres, dont @simon74, définiront ces volumes mieux que moi.
Dernière édition:

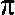 dans le truc et elle va pédaler longtemps...
dans le truc et elle va pédaler longtemps...